kalman fileter

목표

• 칼만필터 파라미터 구하기

---

칼만필터

• 시스템의 상태를 예측하고 추정하는데 사용되는 재귀적인 알고리즘

• 노이즈가 있는 센서 데이터로부터 정확하고 안정적으로 시스템의 상태를 추정하는데 활용

• 구성
  • 예측 단계(Prediction)
    • 이전 상태와 시스템 모델을 기반으로 다음 상태를 예측
    • 또한 시스템 모델과 노이즈에 의해 발생한 불확실성을 고려하여 예측 오차를 계산
  • 업데이트 단계(Update)
    • 실제 센서 데이터를 사용하여 예측된 상태와 실제 상태 사이의 오차를 계산
    • 오차를 이용하여 상태와 오차의 가중치를 조정하고 보정합니다. 이렇게 보정된 상태를 사용하여 다음 예측을 수행

칼만필터 파라미터

• A : A = 1 # 시스템 행렬, 시스템이 어떻게 움직이는 지 나타냄. 즉 시스템의 운동방정식 (n*n)

• H = 1 # 출력 행렬, 측정값과 상태변수의 관계를 나타냄. 즉 측정값에 각 상태 변수가 어떻게 반영되어있는지를 이 행렬이 규정 (m*n)

• Q = 0 # w_k의 공분산 행렬, (n*n) 대각행렬 (w_k : 시스템 잡음, n*1 열벡터)

• R = 4 # v_k의 공분산 행렬, (m*m) 대각행렬 (v_k : 측정잡음, m*1 열벡터 )

칼만필터 식

💡

가속도, 속도, 거리를 측정해보았다.

• 시스템 행렬(System Matrix)
  • 선형 시스템에서 현재 상태와 다음 상태 간의 변화를 설명하는 행렬
  • 선형 시스템은 현재 상태를 시스템 행렬과 입력 벡터의 선형 결합으로 표현
  • 일반적으로 A로 표기되며, 크기는 (n x n)입니다. 여기서 n은 시스템의 상태 변수 개수를 의미
  • 식
    • system matrix : f(x) = Ax + v

• 측정 행렬(Measurement Matrix)
  • 선형 시스템에서 상태 변수를 측정 값으로 변환하는 행렬
  • 선형 시스템은 상태 변수를 측정 행렬과 측정 벡터의 선형 결합으로 표현
  • 일반적으로 C로 표기되며, 크기는 (m x n)입니다. 여기서 m은 측정값의 개수를 의미
  • 식
    • measurement matrix : z(x) = Hx + w

system matrix : f(x) = Ax + v

$$\begin{bmatrix}accel \\velocity  \\ distance \end{bmatrix} = \begin{bmatrix}0 & 0 & 1\\ \triangle t & 0 & 0 \\0 & \triangle t & 1 \end{bmatrix} \begin{bmatrix}aceel \\ velocity \\ distance \end{bmatrix}_{n-1} + \begin{bmatrix} 0.1 \\ 0.2 \\ 0.3 \end{bmatrix}$$

각각의 식을 풀어쓰면 다음과 같음

• $accel = x$

• $velocity = x \triangle t$

• $distance = distance_{n-1} + v \triangle t$

→ 이 시스템 식을 변환하면 위 식이 됨

$\begin{bmatrix}0 & 0 & 1\\ \triangle t & 0 & 0 \\0 & \triangle t & 1 \end{bmatrix}$ ← 이건 A

$\begin{bmatrix} 0.1 \\ 0.2 \\ 0.3 \end{bmatrix}$← 이건 v 적당히 넣기 ( np.eye 해줘서 단위행렬 만들기) → $\begin{bmatrix}0.1 & 0 & 0\\ 0 & 0.2 & 0 \\0 & 0 & 0.3 \end{bmatrix}$, 그 후 Q로 사용!

measurement matrix : z(x) = Hx + w

$$\begin{bmatrix}accel \end{bmatrix} = \begin{bmatrix}1&0&0 \\0&0&0 \\ 0&0&0 \end{bmatrix}\begin{bmatrix}accel \\velocity \\ distance \end{bmatrix} + \begin{bmatrix}1&0&0 \\0&1&0 \\ 0&0&1 \end{bmatrix}$$

$\begin{bmatrix}1&0&0 \\0&0&0 \\ 0&0&0 \end{bmatrix}$ ← H , 가속도만 측정!

$\begin{bmatrix}1&0&0 \\0&1&0 \\ 0&0&1 \end{bmatrix}$← 오차 R. 적당히 넣기

---

system matrix ← hidden Markov process → measurement matrix

system과 measurement matrix는 두개의 방정식이지만, 서로 상관관계가 있음.

def kalman_filter(z_meas, x_esti, P):
    """Kalman Filter Algorithm for One Variable."""
    # (1) Prediction.
    x_pred = A @ x_esti
    P_pred = A @ P @ A + Q
    # (2) Kalman Gain.
    K = P_pred @ H / (H @ P_pred @ H + R)
    # (3) Estimation.
    x_esti = x_pred + K @ (z_meas - H @ x_pred)
    # (4) Error Covariance.
    P = P_pred - K @ H @ P_pred
    return x_esti, P


# Input parameters.
measure_data = x_speed
time_end = len(measure_data)
dt = round(len(df) / (len(measure_data)-1) / 1000, 3)
time = np.arange(0, time_end, dt)

# Initialization for system model.
# 시스템 행렬, 시스템이 어떻게 움직이는 지 나타냄. 즉 시스템의 운동방정식 (n*n)
A = np.array([[1, dt],
              [0, 1]])

# 출력 행렬, 측정값과 상태변수의 관계를 나타냄. 
# 즉 측정값에 각 상태 변수가 어떻게 반영되어있는지를 이 행렬이 규정 (m*n)
H = np.array([[1, 0],
              [1, 0]])

# w_k의 공분산 행렬, (n*n) 대각행렬 (w_k : 시스템 잡음, n*1 열벡터)
Q = np.array([[1, 0], 
             [0, 3]])

# v_k의 공분산 행렬, (m*m) 대각행렬 (v_k : 측정잡음, m*1 열벡터 )
R = np.array([[10]])


peak_diff = np.diff(peakx_list)

# Initialization for estimation.
x_0 = np.array([measure_data[0], peak_diff[0]*dt])  # position and velocity
P_0 = 0.1 * np.eye(2)


n_samples = len(measure_data)
z_pos_meas_save = np.zeros(n_samples)
x_pos_esti_save = np.zeros(n_samples)
x_vel_esti_save = np.zeros(n_samples)

x_esti, P = None, None
for i in range(n_samples):
    z_meas = get_pos_vel(i)
    if i == 0:
        x_esti, P = x_0, P_0
    else:
                                # 실제 속도, 예측한 속도, error
        x_esti, P = kalman_filter(z_meas, x_esti, P)

    print(z_meas,  P)

    z_pos_meas_save[i] = z_meas
    x_pos_esti_save[i] = x_esti[0]
    x_vel_esti_save[i] = x_esti[1]

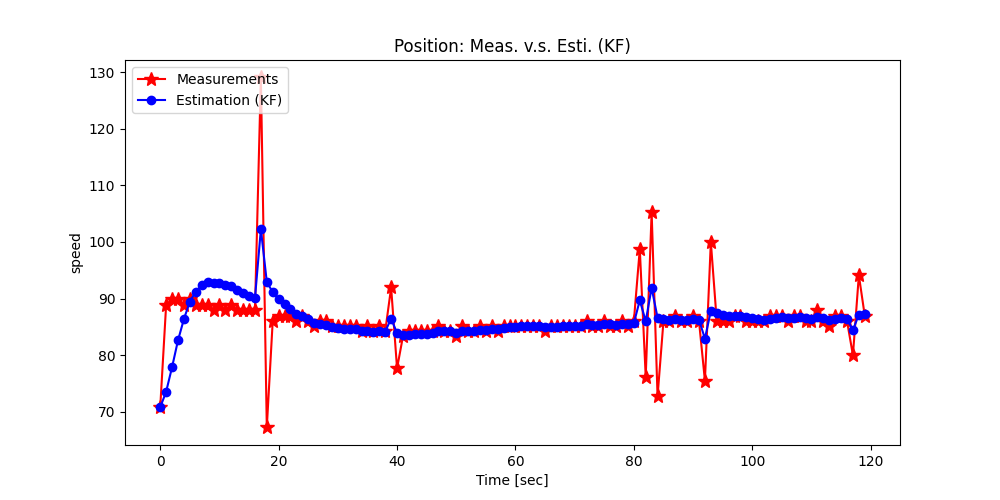
결과 (칼만필터를 이용해 속도 예측)