| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- 카카오
- 코테
- 파이썬을파이썬답게
- python 갯수세기
- PAPER
- Overleaf
- 논문editor
- Tire
- 논문작성
- n_neighbors
- 에러해결
- mMAPE
- 평가지표
- 논문
- knn
- MAPE
- n_sample
- mes
- Mae
- RMES
- Alignments
- KAKAO
- TypeError
- iNT
- 프로그래머스
- 스택
- Pycaret
- Scienceplots
- Python
- SMAPE
- Today
- Total
EunGyeongKim
지도학습 : 회귀_1차원 데이터(선형 기저 함수 모델, 가우시안) (1) 본문
기저함수 : '바탕이 되는 함수' 라는 뜻.
선형회귀모델의 x를 기저함수로 대체해 여러 형태의 함수를 만듦
가우스 함수를 기저함수로 선택한 선형 기저 함수 모델
기저함수는 다음과 같이 표기함.ϕ는 그리스어로 '파일'을 뜻함.
$$\phi_j(x) $$
기저함수는 여러 세트에서 사용되기 때문에 그 번호를 나타내는 J에는 인덱스가 붙어있음. 가우스 기저함수는 다음과 같음
$$\phi_j(x) = exp \left\{ - \frac{(x-\mu_j)^2}{2s^2}\right\}$$
가우스 함수의 중심 위치는 µ_j 임. 함수의 확장 정도는 s로 조절됨. s는 모든 가우스 함수의 공통 매개변수로 함
µ_j , s 는 설계자가 결정하는 매개변수임.
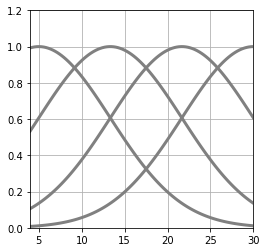
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
# data
np.random.seed(seed =1)
x_min = 4
x_max = 30
x_n = 16
x = 5+24 * np.random.rand(x_n)
prm_c = [170, 108, 0.2]
t = prm_c[0] - prm_c[1] * np.exp(-prm_c[2] *x) + 4*np.random.randn(x_n)
# Gaussian
def gauss(x, mu, s):
return np.exp(-(x-mu)**2/(2*s**2))
# main
m = 4
plt.figure(figsize = (4,4))
mu = np.linspace(5, 30, m)
s = mu[1] - mu[0]
xb = np.linspace(x_min, x_max, 100)
for j in range(m):
y = gauss(xb, mu[j], s)
plt.plot(xb, y, color='gray', linewidth=3)
plt.grid(True)
plt.xlim(x_min, x_max)
plt.ylim(0, 1.2)
plt.show()왼쪽부터 순서대로 ϕ_0(x), ϕ_1(x), ϕ_2(x), ϕ_3(x)이라고 부르자. 이들에 각각 매개변수 w0, w1, w2, w3를 곱해 모두 합한 함수를 다음과 같이 표기함
$$y(x, w) = w_0\phi _0 (x) + w_1\phi _1(x) + w_2\phi _2(x) + w_3\phi _3(x)+w_4$$
이것이 선형 기저함수 모델. 매개변수 w 를 가중치 매개변수라고 함.
마지막 w4는 (=wM)은 곡선 상하의 평행이동. 그러므로 항상 1을 출력하는 ϕ_4(x) = 1 이라고 하는 더미 기초함수 추가 가능. 그 식을 다음과 같이 표기함.
$$y(x, w) = \sum_{j=0}^{m}w_j\phi_j(x) = w^T\phi(x)$$
여기서 w = (w0, w1, ... , w_M)^T, ϕ = (ϕ_-, ϕ_1, ..., ϕ_M)^T를 나타냄. 평균 제곱오차의 식은 다음과 같음
$$J(w) = \frac{1}{N}\sum_{n=0}^{N-1}\left\{ w^T\phi(x_n) - t_n\right\}^2$$
가우시안을 사용한 기저함수의 평균제곱오차는 이전의 선형 평균 제곱오차와 비슷한 모양을 함. 다음이 선형평균 제곱오차임
$$J(w) = \frac{1}{N}\sum_{n=0}^{N-1}(w^Tx_n - t_n)^2$$
즉, 선형기저함수모델은 ϕ(x_n)를 입력 x_n으로 해석한 선형회귀모델과 같음
따라서 J를 최소화하는 매개변수 w는 위의 해석해
$$w = (X^TX)^{-1}X^Tt$$
의 X를 ϕ으로 대체한 다음 식으로 나타낼 수 있음
$$w = (\phi^T\phi)^{-1}\phi^Tt $$
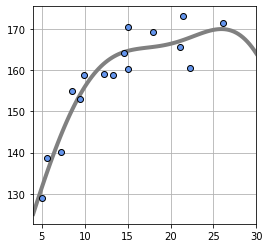
# linear basis function model
def gauss_func(w, x):
m = len(w)-1
mu = np.linspace(5, 30, m)
s = mu[1] - mu[0]
# make y array with same size x
y = np.zeros_like(x)
for j in range(m):
y = y + w[j] * gauss(x, mu[j], s)
y = y+w[m]
return y
# linear basis modeul MSE
def mse_gauss_func(x, t, w):
y = gauss_func(w, x)
mse = np.mean((y-t)**2)
return mse
# exact solution of a linear basis function model
def fit_gauss_func(x, t, m):
mu = np.linspace(5, 30, m)
s= mu[1] - mu[0]
n = x.shape[0]
psi = np.ones((n, m+1))
for j in range(m):
psi[:, j] = gauss(x, mu[j], s)
psi_t = np.transpose(psi)
# 선형대수 함수 (=np.linalg.in)
b = np.linalg.inv(psi_t.dot(psi))
c = b.dot(psi_t)
w = c.dot(t)
return w
# show gauss function
def show_gauss_func(w):
xb = np.linspace(x_min, x_max, 100)
y = gauss_func(w, xb)
# lw = line width
plt.plot(xb, y, c=[.5, .5, .5], lw = 4)
# main
plt.figure(figsize =(4,4))
m =4
w = fit_gauss_func(x, t, m)
show_gauss_func(w)
plt.plot(x, t, marker='o', linestyle='None', color='cornflowerblue', markeredgecolor='black')
plt.xlim(x_min, x_max)
plt.grid(True)
mse = mse_gauss_func(x, t, w)
print('w ='+str(np.round(w, 1)))
print("SD={0:.3f}".format(np.sqrt(mse)))
plt.show()오차의 표준편차는 3.98cm, 직선모델때의 오차 7cm 보다 훨씬 줄어듦.
'ML & DL' 카테고리의 다른 글
| 가우스 함수(Gaussian Function) (0) | 2023.02.23 |
|---|---|
| 지도학습 : 회귀_1차원 모델(선형기저함수_오버피팅, k-fold cross validation) (2) (1) | 2023.02.23 |
| 지도학습 : 회귀_2차원 모델(평면) (0) | 2023.02.22 |
| 지도학습 : 회귀(Regression)_1차원 데이터 선형모델 매개변수의 해석해 (2) (0) | 2023.02.22 |
| 지도학습 : 회귀 (Regression)_1차원 데이터, 직선 (1) (0) | 2023.02.20 |




