Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- SMAPE
- Pycaret
- MAPE
- Tire
- mMAPE
- 스택
- 논문작성
- 에러해결
- 프로그래머스
- Scienceplots
- PAPER
- 파이썬을파이썬답게
- 논문editor
- python 갯수세기
- KAKAO
- 코테
- RMES
- iNT
- Mae
- n_neighbors
- Alignments
- knn
- TypeError
- 평가지표
- 카카오
- Overleaf
- n_sample
- Python
- mes
- 논문
Archives
- Today
- Total
EunGyeongKim
지도학습 : 회귀_1차원 모델(선형기저함수_오버피팅, k-fold cross validation) (2) 본문

plt.figure(figsize =(10, 2.5))
plt.subplots_adjust(wspace = 0.3)
m = [2, 4, 7, 9]
for i in range(len(m)):
plt.subplot(1, len(m), i+1)
w = fit_gauss_func(x, t, m[i])
show_gauss_func(w)
plt.plot(x, t, marker ='o', linestyle = "None", color='cornflowerblue', markeredgecolor='black')
plt.xlim(x_min, x_max)
plt.grid(True)
plt.ylim(130, 180)
mse = mse_gauss_func(x, t, w)
plt.title("m={0:d}, SD={1:.1f}".format(m[i], np.sqrt(mse)))
plt.show()상기 그림처럼 m이 늘어나면 늘어날수록 오버피팅이 됨. 그러므로 test와 train데이터를 나누어 훈련에 사용하지 않는 데이터인 test에 대한 예측오차로 m 평가하기

# train & test data
x_test =x[:int(x_n/4+1)]
t_test =t[:int(x_n/4+1)]
x_train =x[int(x_n/4+1):]
t_train =t[int(x_n/4+1):]
# main
plt.figure(figsize=(10, 2.5))
plt.subplots_adjust(wspace=0.3)
m = [2,4,7,9]
for i in range(len(m)):
plt.subplot(1, len(m), i+1)
w = fit_gauss_func(x_train, t_train, m[i])
show_gauss_func(w)
plt.plot(x_train, t_train, marker='o', linestyle='None', color='white', markeredgecolor='black', label='trainig')
plt.plot(x_test, t_test, marker='o', linestyle='None', color='cornflowerblue', markeredgecolor='black', label='test')
plt.legend(loc='lower right', fontsize = 10, numpoints=1)
plt.xlim(x_min, x_max)
plt.ylim(130, 180)
plt.grid(True)
mse = mse_gauss_func(x_test, t_test, w)
plt.title("m={0:d}, SD={1:.1f}".format(m[i], np.sqrt(mse)))
plt.show()경향을 정량적으로 보기 위해 m을 2~9까지 하나씩 이동하여 훈련데이터와 테스트 데이터 오차(SD)를 그래프로 그려보기

plt.figure(figsize = (5,4))
m = range(2, 10)
mse_train = np.zeros(len(m))
mse_test = np.zeros(len(m))
for i in range(len(m)):
w = fit_gauss_func(x_train, t_train, m[i])
mse_train[i] = np.sqrt(mse_gauss_func(x_train, t_train, w))
mse_test[i] = np.sqrt(mse_gauss_func(x_test, t_test, w))
plt.plot(m, mse_train, marker='o', linestyle='-', color='white', markeredgecolor='black', label='trainig')
plt.plot(m, mse_test, marker='o', linestyle='-', color='cornflowerblue', markeredgecolor='black', label='test')
plt.legend(loc='lower right', fontsize = 10)
plt.show()오차는 감소하다가 5부터 다시 증가하고 있음. 즉 m=5에서 오버피팅이 일어나고 있다고 할 수 있음. 그러므로 m=4일떄 가장 적합하다고 할 수 있음.
k겹 교차 검증(k-fold cross validation)
데이터를 k개로 분할하여 각 데이터셋 마다 오차를 계산하여 평균내어 m 구하기.
# k fold cross validation
def kfold_gauss_func(x, t, m, k):
n= x.shape[0]
mse_train = np.zeros(k)
mse_test = np.zeros(k)
for i in range(0, k):
# fmod = n을 k로 나눈 나머지를 출력함
x_train = x[np.fmod(range(n), k) != i]
t_train = t[np.fmod(range(n), k) != i]
x_test = x[np.fmod(range(n), k) == i]
t_test = t[np.fmod(range(n), k) == i]
wm = fit_gauss_func(x_train, t_train, m)
mse_train[i] = mse_gauss_func(x_train, t_train, wm)
mse_test[i] = mse_gauss_func(x_test, t_test, wm)
return mse_train, mse_test
# main
m = range(2, 8)
k = 16
cv_gauss_train = np.zeros((k, len(m)))
cv_gauss_test = np.zeros((k, len(m)))
for i in range(0, len(m)):
cv_gauss_train[:, i], cv_gauss_test[:, i] = kfold_gauss_func(x, t, m[i], k)
mean_gauss_train = np.sqrt(np.mean(cv_gauss_train, axis = 0))
mean_gauss_test = np.sqrt(np.mean(cv_gauss_test, axis = 0))
plt.figure(figsize = (4, 3))
plt.plot(m, mean_gauss_train, marker = 'o', linestyle='-', color='white', markeredgecolor='black', label='trainig')
plt.plot(m, mean_gauss_test, marker = 'o', linestyle='-', color='cornflowerblue', markeredgecolor='black', label='test')
plt.legend(loc = 'upper left', fontsize=10)
plt.ylim(0, 20)
plt.grid(True)
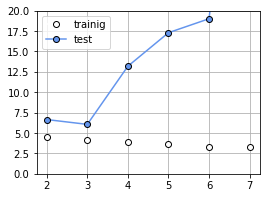
plt.show()LOOCV(leave one out cross validation)일 때 m= 3이 가장 적합함.
데이터 수가 많으면 교차검증에 시간이 많이 걸림.
'ML & DL' 카테고리의 다른 글
| 활성화 함수(Activation Function) 종류 (0) | 2023.03.03 |
|---|---|
| 가우스 함수(Gaussian Function) (0) | 2023.02.23 |
| 지도학습 : 회귀_1차원 데이터(선형 기저 함수 모델, 가우시안) (1) (0) | 2023.02.23 |
| 지도학습 : 회귀_2차원 모델(평면) (0) | 2023.02.22 |
| 지도학습 : 회귀(Regression)_1차원 데이터 선형모델 매개변수의 해석해 (2) (0) | 2023.02.22 |
Comments




