| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- Overleaf
- SMAPE
- Mae
- mes
- Pycaret
- MAPE
- 스택
- RMES
- KAKAO
- 에러해결
- Alignments
- TypeError
- Python
- Tire
- Scienceplots
- 논문
- 코테
- iNT
- 논문editor
- python 갯수세기
- n_neighbors
- n_sample
- 평가지표
- 프로그래머스
- 카카오
- 파이썬을파이썬답게
- 논문작성
- mMAPE
- PAPER
- knn
- Today
- Total
EunGyeongKim
지도학습 : 분류 본문
Ref :파이썬으로 배우는 머신러닝의 교과서
곤충의 무게를 분류하는 식.
데이터는 random 으로 만든다. 무게는 \(x_n \), 성별을 \( t_n \) 으로 나타냄. \( t_n \)은 0(암컷) 또는 1(수컷)을 갖는 변수
무게를 기초로 성별을 예측 및 분류하는 모델.
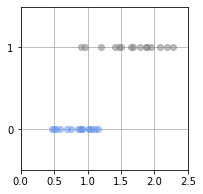
곤충의 무게를 분류하는 식.
데이터는 random 으로 만든다. 무게는 \(x_n \), 성별을 \( t_n \) 으로 나타냄. \( t_n \)은 0(암컷) 또는 1(수컷)을 갖는 변수
무게를 기초로 성별을 예측 및 분류하는 모델.
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline
np.random.seed(seed=0)
X_min = 0
X_max = 2.5
X_n = 30
X_col = ['cornflowerblue', 'gray']
X = np.zeros(X_n)
T = np.zeros(X_n, dtype=np.uint8)
Dist_s = [0.4, 0.8]
Dist_w = [0.8, 1.6]
Pi = 0.5
for n in range(X_n):
wk = np.random.rand()
T[n] = 0 * (wk < Pi) + 1 * (wk >= Pi) #(A)
X[n] = np.random.rand() * Dist_w[ T[n] ] + Dist_s[ T[n] ]
def show_data1(x1,t1):
K = np.max(t1) + 1
for k in range(K): #(A)
plt.plot( x1[t1==k], t1[t1==k], X_col[k], alpha=0.5, linestyle='none', marker='o' ) #(B)
plt.grid(True)
plt.ylim(-.5, 1.5)
plt.xlim(X_min,X_max)
plt.yticks([0,1])
fig = plt.figure(figsize=(3,3))
show_data1(X, T)
plt.show()
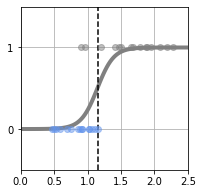
암컷이 될 확률은 Pi=0.5이며 무작위로 결정됨. 분류문제를 푸는 방법은 수컷과 암컷을 분리하는 경계선을 그리는것.
0.8 미만일때는 암컷, 1.2 이상일때는 수컷으로 분류할 수 있지만 0.8 ~ 1.2 사이라면 분류가 어려워짐.
확률을 사용하여 경계선을 예측 하기
x에 대해 수컷일 확률은(t=1) 조건부 확률을 사용하여 \( P(t = 1| x) \) 의 식으로 나타낼 수 있음.
조건부확률 : 어떤 사건이 일어나는 경우에 다른 사건이 일어날 확률을 말함.
\( P(A|B) \) 라고 표기하며 사건 B가 일어나는 경우에 사건 A가 일어나는 경우
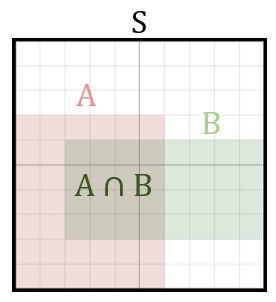
\( P(A|B) = \frac{P(A\cap B)}{P(B)} = \frac{\frac{n(A \cap B)}{n(S)}}{\frac{n(B)}{n(S)}} \)
\( = \frac{n(A\cap B)}{n(B)} \)
사건 B가 일어났을 경우 사건 A가 일어날 확률은, 사건 B가 일어날 확률에서 사건 A, B가 동시에 일어날 확률이 차지하는 비중. 집함B의 원소들이 얼마나 많이 집합 A에 해당하는지 나타낸다고 할 수 있음.
최대가능도법을 이용하여 경계선 예측하기
예제 : \( t_1 = 0 \), \( t_2 = 0 \), \( t_3 = 0 \), \( t_4 = 1 \) 일때 0.8 < x <= 1.2로 \( P(t=1|x) \) 추정해 보기
1. 먼저 단순한 모델( \(P(t=1|x)=w \) ) 먼저 고려하기
위 모델은 확률 w에서 t = 1을 생성하는 모델. w의 범위는 0~1사이
모델이 t = 0,0,0,1이라는 데이터를 생성하였다고 가정할때, 이 정보를 통해 가장 타당한 w를 추정하는 문제 고려해야함.
't = 0,0,0,1이 생성될 확률'을 우도 라고 함
w가 0.1일 경우의 가능도 \( w = P(t =1|x)=0.1 \) 이므로 t가 될 확률은 1-0.1 = 0.9가 됨. 그러므로 t가 0,0,0,1이 될 확률은 0.9 * 0.9 * 0.9 * 0.1 = 0.0729 가 됨
같은 방법으로 w가 0.2일 경우의 가능도 \( w = P(t =1|x)=0.2 \) 이므로 t가 될 확률은 1-0.2 = 0.8가 됨. 그러므로 t가 0,0,0,1이 될 확률은 0.8 * 0.8 * 0.8 * 0.2 = 0.0024 가 됨
w = 0.1과 w = 0.2일 가능도를 비교했을때 w = 0.2 의 확률이 더 높음. 이 방법을 이용하여 최대가 되는 w를 구하면 됨
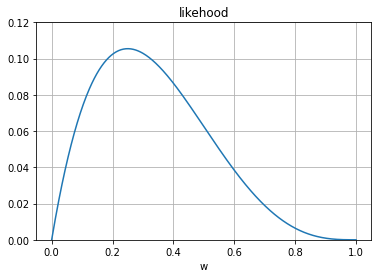
import math
def likehood(w):
y = (1-w)**3 * w
return y
x = np.linspace(0, 1, 501)
y = likehood(x)
plt.plot(x, y)
plt.grid()
plt.ylim(0, 0.12)
plt.xlabel('w')
plt.title('likehood')
plt.show()
print('max: ',max(y),'max w: ',x[np.where(y == max(y))[0][0]] )
로지스틱 회귀 모델을 이용하여 예측해 보기
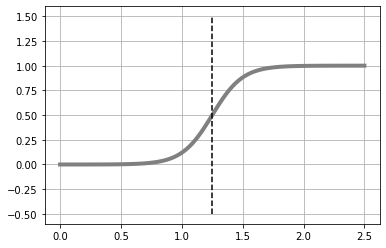
def logistic(x,w):
y = 1 / ( 1 + np.exp( -(w[0] * x + w[1])) )
return y
def show_logistic(w):
xb = np.linspace(X_min, X_max, 100)
y = logistic(xb, w)
plt.plot(xb, y, color='gray', linewidth=4)
#결정 경계
i = np.min( np.where(y > 0.5) ) #(A)
B = (xb[i - 1] + xb[i]) / 2 #(B)
plt.plot([B, B], [-.5, 1.5], color='k', linestyle='--')
plt.grid(True)
return B
# test
W = [8, -10]
show_logistic(W)교차 엔트로피 오차
로지스틱 회귀모델을 통해 x가 t=1이 될 확률을 다음과 같이 나타냄.
$$y = \sigma(w_0x+ w_1) = P(t=1|x)$$
매개변수 \(w_0 \), \(w_1 \)이 곤충 데이터에 맞도록 최대 가능도법을 활용함.
최대가능도법은 다음 방법을 이용하여 구할 수 있음.
- 곤충의 데이터가 이 모델에서 생성될 확률, 가능도를 구함
- 이 생성 확률을 수학적인 트릭을 사용하여 다음과 같이 나타냄.
$$ P(t|x) = y^t (1-y)^{1-t} $$
- t=1 인경우 다음 식과 같음.
$$P(t=1|x) = y^1 (1-y)^{1-1} = y$$
- t=0인경우 다음 식과 같음.
$$P(t=0|x) = y^0(1-y)^{1-0} =1- y$$
- 데이터가 N개라면 생성 확률은 다음과 같음.
$$P(T|X) =\prod_{n=0}^{N-1} P(t_n | x_n) = \prod_{n=0}^{N-1} y_n^{t_n}(1- y_n)^{1-t_n}$$
- 식에 -1를 곱한 이유는 평균 제곱오차가 최소가 되도록 매개변수를 구하고 있었기 때문. 이를 교차엔트로피 라고 함.
$$P(T|X) =\prod_{n=0}^{N-1} \{ t_n log y_n + (1-t_n)log(1-y_n) \}$$
- 평균 교차 엔트로피 E(w)로 정의 (N으로 나눈 값)
$$E(w) = - \frac{1}{N}logP(T|X) = -\frac{1}{N}\prod_{n=0}^{N-1} \{ t_nlogy_n+(1-t_n)log(1-y_n) \}$$
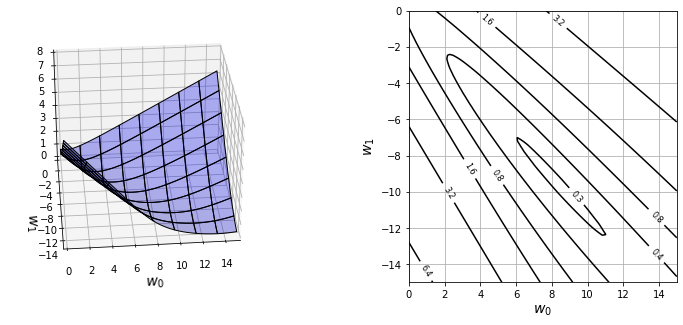
from mpl_toolkits.mplot3d import Axes3D
#cal
xn = 80
w_range = np.array([ [0,15], [-15, 0] ])
x0 = np.linspace( w_range[0,0], w_range[0,1], xn )
x1 = np.linspace( w_range[1,0], w_range[1,1], xn )
xx0, xx1 = np.meshgrid(x0, x1)
C = np.zeros( (len(x1), len(x0)) )
w = np.zeros(2)
for i0 in range(xn):
for i1 in range(xn):
w[0] = x0[i0]
w[1] = x1[i1]
C[i1, i0] = cee_logistic(w, X, T)
# show
plt.figure(figsize=(12,5))
plt.subplots_adjust(wspace=0.5)
ax = plt.subplot(1,2,1,projection='3d')
ax.plot_surface(xx0, xx1, C, color='blue', edgecolor='black', rstride=10, cstride=10, alpha=0.3)
ax.set_xlabel('$w_0$', fontsize=14)
ax.set_ylabel('$w_1$', fontsize=14)
ax.set_xlim(0, 15)
ax.set_ylim(-15, 0)
ax.set_zlim(0, 8)
ax.view_init(30, -95)
plt.subplot(1,2,2)
cont = plt.contour(xx0, xx1, C, 20, colors='black', levels=[0.26, 0.4, 0.8, 1.6, 3.2, 6.4])
cont.clabel(fmt='%1.1f', fontsize=8)
plt.xlabel('$w_0$', fontsize=14)
plt.ylabel('$w_1$', fontsize=14)
plt.grid(True)
plt.show()최소치는 \( w_0 \) =9, \( w_1 \) = -9 근처에 있음.
로지스틱 회귀 모델이 의한 피팅 결과
# 평균 교차 엔트로피의 오차 미분
def dcee_logistic(w,x,t):
y = logistic(x,w)
dcee = np.zeros(2)
for n in range(len(y)):
dcee[0] = dcee[0] + ( y[n] - t[n] ) * x[n]
dcee[1] = dcee[1] + ( y[n] - t[n] )
dcee = dcee / X_n
return dcee
#경사 하강법에 의한 값.
from scipy.optimize import minimize
def fit_logistic(w_init, x, t):
res1 = minimize(cee_logistic, w_init, args=(x, t),
jac=dcee_logistic, method="CG") # (A)
return res1.x
# 메인 ------------------------------------
plt.figure(1, figsize=(3, 3))
W_init=[1,-1]
W = fit_logistic(W_init, X, T)
print("w0 = {0:.2f}, w1 = {1:.2f}".format(W[0], W[1]))
B=show_logistic(W)
show_data1(X, T)
plt.ylim(-.5, 1.5)
plt.xlim(X_min, X_max)
cee = cee_logistic(W, X, T)
print("CEE = {0:.2f}".format(cee))
print("Boundary = {0:.2f} g".format(B))
plt.show()'ML & DL' 카테고리의 다른 글
| 정규분포(normal distribution) (0) | 2023.03.22 |
|---|---|
| 백분위수, 사분위수 (0) | 2023.03.22 |
| 활성화 함수(Activation Function) 종류 (0) | 2023.03.03 |
| 가우스 함수(Gaussian Function) (0) | 2023.02.23 |
| 지도학습 : 회귀_1차원 모델(선형기저함수_오버피팅, k-fold cross validation) (2) (1) | 2023.02.23 |





