💡
차량의 wheel alignments을 위한 camber angle 검사(MCU 기반3축 가속도 센서)
wheel alignment의 중요성
- Toe angle
- 연료 효율성, tire lifespan, driving comfort에 영향을 줌.
접근 방법
- MCU기반 접근방식은 3축 가속도 센서를 이용해 중력값을 획득하고, camber 검사 시스템와 차량간의 좌표변환을 적용시킴
- 캠버 시스템의 오정렬 각도를 자체적으로 보상할 수 있으므로, X축과 Z의 캠버축 완벽한 각도 조절이 필요하지 않음.
- 본 논문에서의 데카르트 좌표 C의 구성요소를 다음과 같이 표현함
⎝⎛xCyCzC⎠⎞C=[iC jC kC]⎣⎡xCyCzC⎦⎤ - iC : 직교좌표 C의 x축 unit vector
- jC : 직교좌표 C의 y축 unit vector
- kC : 직교좌표 C의 z축 unit vector
- (xC,yc,zC)CT : 직교좌표 C의 벡터를 나타냄
- [xC,yC,zC]T : 벡터에 따른 3x1 매트릭스
- 이 논문에서 C는 차량, 바퀴, 가속도계 또는 캠버 검사 시스템이 될 수 있음.
차량과 캠버 검사 시스템의 좌표 변환
- 캠버 검사 시스템은 좌표 S의 캠버 검사 시스템에서 로컬 중력(1g = 9.8m/s2와 같지는 않음)를 감지 할 수 있지만, 로컬중력은 차량좌표 V의 아래쪽에만 있음.
- 좌표 V와 S사이의 좌표 변환은 로컬 중력이 좌표 V와 S에 따라 다른 표현을 가진 동일한 벡터임
- 그림 2는 좌표 V를 보여줌
- 좌표V의 x, y, z축은 각각 전방, 우측, 하향으로 정의됨.
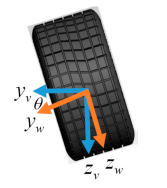 front view of the vehicle and wheel coordinates with the pitch (camber) angle
front view of the vehicle and wheel coordinates with the pitch (camber) angle
- 시스템 주축과 정렬된 좌표 S의 x,y, z.
⇒ 좌표 S을 이용해 캠버각도 측정
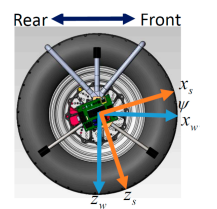 right side view of the front-right wheel and the camber inspection system with yaw angles.
right side view of the front-right wheel and the camber inspection system with yaw angles.
- pitch각도와 yaw각도를 포함하여 좌표 V와 S사이의 오일러 각은 좌표 변환에 필요함.
- camber각도는 분명히 pitch 각도 θ임
- yaw 각도 ψ 는 좌표 S의 x축과 휠좌표 W가 어긋난 각도임.
- 중력과 같은 물체는 다른 좌표에 있을 수 있음.
⎝⎛xVyVzV⎠⎞V=⎝⎛xWyWzW⎠⎞W or
[iV,jV,kV] ⎣⎡xVyVzV⎦⎤= [iW,jW.kW] ⎣⎡xWyWzW⎦⎤
- 정의에 따르면 그림 2의 좌표는 좌표 V와 W에 의해 변환됨 (1)
⎣⎡xVyVzV⎦⎤=⎣⎡1000cosθsinθ0−sinθcosθ⎦⎤⎣⎡xWyWzW⎦⎤
- 비슷하게 그림3에서의 정의는 좌표 W와 S사이에서 좌표 변환이 일어남. (2)
⎣⎡xWyWzW⎦⎤=⎣⎡cosψ0−sinψ010sinψ0cosψ⎦⎤⎣⎡xSySzS⎦⎤ - θ는 좌표 V가 좌표 W로 각도가 회전되었음
- ψ은 좌표 W에서 S로 회전되었음
- 식 2에서 1을 빼면 좌표 V에서 S로의 좌표변환은 다음과 같음 (3)
⎣⎡xVyVzV⎦⎤=⎣⎡cosψsinθsinψ−cosθsinψ0cosθsinθsinψ−sinθcosψcosθcosψ⎦⎤⎣⎡xSySzS⎦⎤
캠버 각도 검사와 오류 분석
- 로컬 중력은 가속도계의 가속도에 의해 감지 될뿐임
- 가속도계는 가속도 a=axis+ayjS+azkS를 획득할 수 있음
- 여기서 ax, ay, az는 각각 좌표 S의 x, y, z 성분의 가속도
⎝⎛00g⎠⎞V=⎝⎛axayaz⎠⎞S ψ=−tan−1azax θ=tan−1azcosψ−axsinψay θ=tan−1ax2+az2ay - 제안된 접근방식에서 캠버각도 측정은 좌표 S와 좌표 W 사이의 misaligned 각도 ψ와 무관함
- 또한 misaligned 된 각도는 식 (4)로부터 평가할 수 있음
- 바퀴의 캠버각도 θ는 가속도계에서 감지된 가속도가 준비되어 있음
- 식 (6)에서 좌표 S와 W의 X축이 완전히 같은 방향으로 정렬되어 있는지의 여부를 직업 판단할 수 있음.
캠버 검사 시스템과 가속도계 사이의 오정렬된 축에 대한 보정
- 캠버 검사 시스템과 가속도계사이의 오정렬된 축은 보통 MCU기반 캠버 검사 시스템에 관해서 발생함
- xk,i yk,i, zk,i는 가속도계에서 측정된 값을 나타냄
- k는 x, y, z일 수 있으며, 시스템의 k축 보정에 대한 인덱스임
- i는 1~N까지의 범위를 가지면서 i번째 set data의 인덱스임
- xk, yk, zk는 평균 중력에 의해 제약된 최소제곱성능을 갖는 N데이터의 xk,i, yk,i, zk,i각각에 대한 최적 추정값을 나타냄
J=i=1∑N(xk−xk,i)2+i=1∑N(yk−yk,i)2+i=1∑N(zk−zk,i)2 g(xk,yk,zk)=xk2+yk2+zk2−N2(∑i=1Nxk,i2+yk,i2+zk,i2)2=0 - 식 7, 8은 제약조건이 있는 최적화 문제. 라그랑주(Lagrange) 함수는 다음과 같음.(9)
L(xk,yk,zk+λk)=i=1∑N(xk−xk,i)2+i=1∑N(yk−yk,i)2+i=1∑N(zk−xz,i)2+λk(xk2+yk2+zk2−N2(∑i=1Nxk,i2+yk,i2+zk,i2)2) - λk는 라그랑주 승수 . ∂xk∂L=0,∂yk∂L=0,∂zk∂L=0,∂λk∂L=0은 (9)번식의 최적 조건 (10),(11),(12)
xk=N+λk∑i=0Nxk,i
yk=N+λk∑i=0Nyk,i zk=N+λk∑i=0Nzk,i λk=N(∑i=1Nxk,i2+yk,i2+zk,i2(∑i=1Nxk,i)2+∑i=1Nyk,i)2+∑i=1Nzk,i)2−1) - 13번 식에 따라 (14), (15), (16)
xk=N∑i=1Nxk,i(∑i=1Nxk,i)2+(∑i=1Nyk,i)2+(∑i=1Nzk,i)2∑i=1Nxk,i2+yk,i2+zk,i2 yk=N∑i=1Nyk,i(∑i=1Nxk,i)2+(∑i=1Nyk,i)2+(∑i=1Nzk,i)2∑i=1Nxk,i2+yk,i2+zk,i2 zk=N∑i=1Nzk,i(∑i=1Nxk,i)2+(∑i=1Nyk,i)2+(∑i=1Nzk,i)2∑i=1Nxk,i2+yk,i2+zk,i2 - 예를 들어 캠버 검사 시스템의 x축 보정 시 그림4와 같이 시스템이 수직면에 기대어 있는 동안 x축은 수직으로 지면을 향함. 가속도계에서 3축 가속도 측정 데이터를 순차적으로 수집할 수 있음. (17)

⎝⎛100⎠⎞s=⎝⎛xxyxzx⎠⎞A - A는 xx=xx2+yx2+zx2xx, yx=xx2+yx2+zx2yx , zx=xx2+yx2+zx2zx일때 좌표 A의 가속도계
- 시스템의 z축 조정은 다음과 같은 순서로 진행됨 (18)
⎝⎛001⎠⎞s=⎝⎛xxyxzx⎠⎞A - vertical 평면에서의 x축과 z축은 캠버 검사 시스템의 back plane을 위해 조정 될 수 있음.
- x축과 ,z축이 충족되면, 17번 식과 18번 식으로부터 내적연산 결과(xxxz+yxyz+zxzz=0)
⎝⎛010⎠⎞s=⎝⎛xyyyzy⎠⎞A - 여기서 (xy,yy,zy)AT=(xz,yz,zz)AT×(xx,yx,zx)AT . 결과적으로
⎝⎛axayaz⎠⎞S=⎝⎛axaayaazab⎠⎞A ⎣⎡axayaz⎦⎤=⎣⎡xxyxzxxyyyzyxzyzzz⎦⎤−1⎣⎡axaayaaza⎦⎤
- 즉, 캠버 검사 시스템의 해당 가속도로 변환될 수 있는 axa,aya,aza가 가속도에서 측정된 데이터.
- 따라서 정밀한 보정을 통해 시스템과 가속도계 축의 misaligned를 제거할 수 있음.
- 또한 캠버각은 식 19로 변환된 가속도계 좌표에 의한 원시 측정 데이터로 식 6으로부터 측정될 수 있음.
에러분석 측정
- 식 (6)에서 캠버각도 dθ의 미분은 다음과 같이 계산됨 (20)
dθ=ax2+ay2+az21(−sinθsinψdax+cosθday−sinθcosψdaz) - dax,day,daz는 각각 x, y, z축의 간격임.
- 캠버 검사 시스템에서 감지된 가속도는 로컬 중력(1g)과 같음.
ax2+ay2+az2≅g2 dθ≅g1(−sinθsinψdax+cosθday−sinθcosψdaz) - (21)식에서 오른쪽 식의 부호가 모두 +인 악조건에서 방정식 (21)은 다음과 같이 표현함 (22)
∣dθ∣≅g1(∣sinθsinψdax∣+∣cosθday∣+∣sinθcosψdaz∣) - 식(22)는 camber측정의 오류가 모든 가속도 축의 간격에 높게 의존함을 설명함.
- 식(22)의 악조건에서의 최소 측정 에러는 θ=0일때 day와 중력의 비율과 같음 (23)
θψmin∣dθ∣=g∣day∣ - 일반적으로 가속도계의 3축 간격은 동일하지 않음
- 식 (23)은 측정 오류를 줄이기 위해 가속도계의 최선의 간격 축이 좌표 S의 y축에 가깝게 정렬되어야함을 의미하는것으로 해석 가능함.
- 식 (22)의 측정오차는 캠버 각도 및 오정렬 또는 좌표 V에 대한 좌표의 attitude에 따라 달라짐.
- 식 (22)를 기반으로 그림 5는 가속도 측정의 악조건 상태인 dax=day=daz=±4mg(4mg는 가속도계의 감도임)의 경우 θ와 ψ의 차이의 캠버각도 측정 오류를 그림
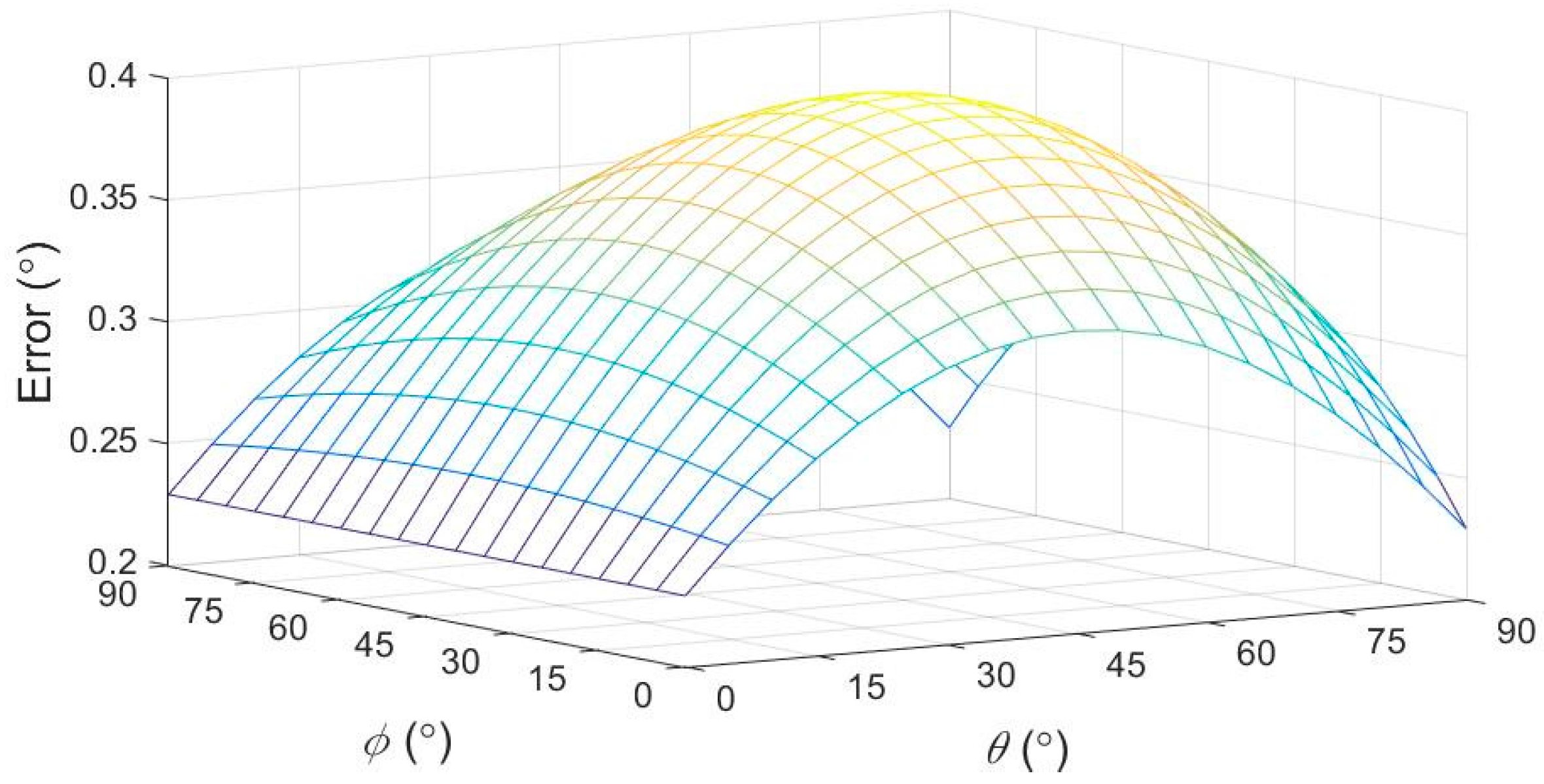
- 방정식 (23)에서 θ=0일때 최소 측정 오차는 0.2292∘
- 캠버각도는 θ≅0 일때 0 근처임





